Algorithms in Motion: Elementary Cellular Automata in Max and Max for Live

Even though my background is largely in theatre, I've always been interested in math. To me, theatre is about digging into the subjectivity of truth, but math always felt like an effort to objectivize. There is still poetry in it, though -- as a kid, geometry particularly felt like a balanced carrier for head and heart.
As I became more interested in music, I found that things felt best when my creative process had the same head/heart balance. Too often, I found that the more I exercised will and control (as if I was somehow going to compose a never-before-heard melody), the less healing music became. Infusing ego stripped the fundamental experience that making music naturally provides -- the one which rewards curiosity and makes you feel happily small against the full scope of nature.
It's funny how many breadcrumbs are scattered through the landscape of open source music technology. A bit of code can act very much like a score -- it is not only an individual expression of an idea , but it encapsulates the possibilities of that idea. It's both an expression of self, like any piece of art, and a tool that can be repurposed, remixed, and reframed to fit the unique needs of a wide range of artists.
The code that struck me
Ezra Buchla's implementation of 1-d cellular automata for monome's Teletype has been one of the most impactful bits of code for me. At its core, it's a simple adaptation of the elementary cellular automata initially described by Stephen Wolfram in his groundbreaking book A New Kind of Science.
The celllular automata start with a fixed set of combinations:
[111] [110] [101] [100] [011] [010] [001] [000]
Choose a rule between 0 and 255, which is converted into an 8-bit binary value:
rule 30 = 0 0 0 1 1 1 1 0
This becomes the output of our combinations:
[111] [110] [101] [100] [011] [010] [001] [000]
0 0 0 1 1 1 1 0Choose an initial seed between 0 and 255 and it'll also be converted into an 8-bit binary integerseed 36 = 0 0 1 0 0 1 0 0
And these binary bits are then grouped into trios (with the edges wrapped):
group 1 (0 0 1 0 0 1 0 0) = [000]
group 2 (0 0 1 0 0 1 0 0) = [001]
group 3 (0 0 1 0 0 1 0 0) = [010]
group 4 (0 0 1 0 0 1 0 0) = [100]
group 5 (0 0 1 0 0 1 0 0) = [001]
group 6 (0 0 1 0 0 1 0 0) = [010]
group 7 (0 0 1 0 0 1 0 0) = [100]
group 8 (0 0 1 0 0 1 0 0) = [000]
We then compare these trios against the fixed combinations and build a new number from the output:
[111] [110] [101] [100] [011] [010] [001] [000]
0 0 0 1 1 1 1 0[000] -> 0
[001] -> 1
[010] -> 1
[100] -> 1
[001] -> 1
[010] -> 1
[100] -> 1
[000] -> 00 1 1 1 1 1 1 0 = 126
That new number becomes our next state! In the case of this example, 126 [0 1 1 1 1 1 1 0] will be re-seeded to be processed against our rule in the same way.
Inherently musical
This iterative processing of rules and seeds maps really nicely to compositional needs for several reasons:
Ones and zeros make for excellent rhythm generators (1 = note, 0 = no note).
Repetition projects a kind of intentionality — as we iterate through our states, we eventually re-seed the initial seed and we wind up with a loop.
Some rule + seed combinations terminate very quickly as they iterate, resulting in a pleasing stasis of silence or single repeating notes.
Making it in Max
I decided to replicate this functionality in Max. To do so, we'll need to tackle the following tasks:
Convert numbers to 8-bit binary (for both the rules and the seeds)
Compare eight groups of three bits each to yield a single bit from each group
Group the eight resulting bits and convert the 8-bit binary back to a number (our output and re-seeding)
Converting numbers to 8-bit binary
We'll use Max's & (bitwise intersection) and >> (right shift) objects to assist with this task. Performing a bitwise intersection of two values involves comparing the bits of two numbers, finding where they have matching1 's. We then output the result to the >> object, which moves all the bits of the number to the right. In binary arithmetic, this has same effect as dividing a number by a power of 2.
This pairing of bitwise intersection with shifting lets us extract individual binary bits from an integer.
Here's a Max patch that processes rule 30 and sending its bits off to storage:

And here's the a partch processing a seed value of 36:

Comparing eight groups of three bits each to yield a single bit from each group
To help us group these binary output bits into trios, we'll use the pak object (which triggers output whenever any of the individual binary output bits change). As in the original example, these binary bits are grouped into trios (with the edges wrapped):
group 1 (0 0 1 0 0 1 0 0) = [000]
group 2 (0 0 1 0 0 1 0 0) = [001]
group 3 (0 0 1 0 0 1 0 0) = [010]
group 4 (0 0 1 0 0 1 0 0) = [100]
group 5 (0 0 1 0 0 1 0 0) = [001]
group 6 (0 0 1 0 0 1 0 0) = [010]
group 7 (0 0 1 0 0 1 0 0) = [100]
group 8 (0 0 1 0 0 1 0 0) = [000]Here's the Max patch that handles the grouping:

Next, we'll compare them to our fixed set of combinations and output the relevant bit from our rule if there's a match:

Group the eight resulting bits and convert the 8-bit binary back to a number (our output and re-seeding)
From here, we convert our result back to integer values by left bitshifting and performing another bitwise intersection:
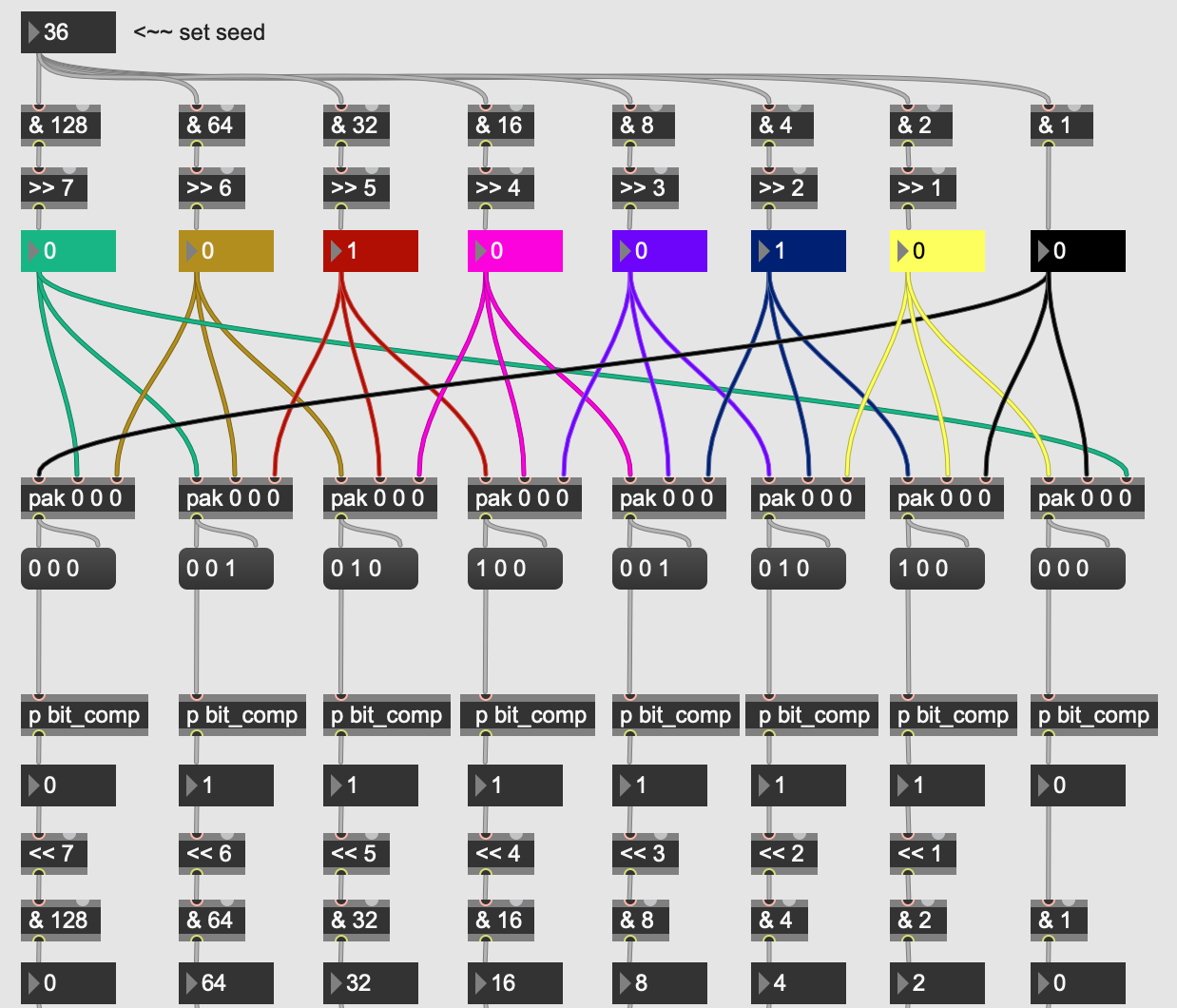
Finally, we sum up the integers to get our next state (126, in this example) and then feed that number back in to get a loop of values!

The results of this process can be used in lots of ways:
You could use a scale object to scale the values to the 0.-1. range used for Vizzie or VST parameter values.
You could use the the streams of ones and zeros to trigger samples.
You could use the raw output to control a group of mc objects
Since the output is relatively agnostic, it can be turned into anything!
How I use it
I've packed this patcher up into a Max for Live device called less concepts, which places bounds on these looping sequences to clamp them to useful MIDI ranges and creates gates out the iterating number's binary bits.
The primary goal of the device is to expose a few useful musical parameters to the stream of bits and integers. For those who have worked with cellular automata in the past, this approach definitely yields less "complex random" than those which employ wider ranges. This limitation has actually proved rather rewarding -- it doesn't take too long to learn the "melody" of rule 30 / seed 36.
Rather than extend the complexity of the engine, I opted to add power to the controls surrounding it. In homage to Laurie Spiegel's Music Mouse, there is a 'laurie' mode which adds chord voicing to the bit streams. Similarly, 'olafur' mode takes its name from Olafur Arnalds (and his custom software, Stratus), which allows the user to redefine the currently iterating scale with chord shapes on their keyboard.
And as a final tie-in to Teletype, the Max for Live version of less concepts features a text-based tracker-style sequencer with a custom set of operators, provides direct control over changing rules, seeds, bits, octaves, clock speed, scales, as well as itself.
In his book A New Kind of Science, Stephen Wolfram states his belief that complex events are actually the result of simple systems working alongside each other.
With that idea in mind, here's a quick demo that highlights how simply changing bits, seeds, and octaves every so often can lead to musical patterns:
Give it a go
I hope you've found a little bit of inspiration here, whether it involves incorporating this version of elementary cellular automata into your projects, downloading and working with the less concepts Max for Live device, or encouraging you to take a stab at porting inspiration from those whose work you admire into your own projects.
Downloading:
less concepts: Max for Live device and PDF guide
Further listening:
Dan Derks' 2018 album less concepts
Further reading:
Laurie Spiegel's Manipulations of Musical Patterns
Stephen Wolfram's A New Kind of Science
by dan derks on April 28, 2020


