An MC Journey, Part 3

One of you kind souls out there emailed to ask me why I titled this series of MC tutorials with the word "journey. " That question is a perfect place to start this particular tutorial.

I used the term as a way to play with your expectations as a reader. The word "tutorial" has always suggested to me that there’s fixed (or organized) information in play, and it’s also often the case that that information is aimed at someone who either knows next to nothing or someone who knows everything but the tutorial’s specific information. In my experience, there’s a universe of difference between those two points, and it seems that we seldom make the process of learning by going where to go a part of the subject. I decided that I’d structure my MC tutorials to represent how I try to make my way not from ignorance to mastery, but from ignorance to idiosyncrasy. Because that’s how I really work, and I suspect that that’s true of a lot of you, too. I wanted this particular series of "tutorials" to include ideas such as "Your mistakes can lead you somewhere interesting" or "There's nothing wrong with building patches to help you to figure something out - they can be a starting point for something else."

Thanks for being willing to follow along in this series (even when I’ve gone places that might not be points along your path). I’ve tried to take some shortcuts by borrowing liberally from earlier tutorials I’ve done here because it saves time, and also because that, too, is how I usually work. Let's get down to it.

The things you pass by and the things you return to

The first part of this series on exploring MC began with my trying to figure out how a feature of the amazing MC tools worked, making a patch to explore it, and suddenly seeing something that sent me off in a direction I hadn’t anticipated, which became the second part of the series. Not exactly the stuff of a linear tutorial, huh?

In terms of figuring out the MC spread, spreadinclusive, and spreadexclusive messages, I realized at some point that I was looking at floating-point numbers that described something specific - frequency ratios - rather than interestingly spaced number values given low and high range information. While I’d like to claim that I saw that the second I had my little spreader investigation patch up and running for the first time, I’d be lyin’, pure and simple.

In truth, it didn’t happen until I saw a very specific number come up when typing low and high values in and selecting the kind of spread message to apply (If you’re curious, the number was 15/8 or 1.875, which is a major seventh interval in Just Intonation - an interval I really like). Looking back on that moment of insight now, I feel a little silly… I’d been staring at perfect fifths (3/2 or 1.5), perfect fourths (4/3 or 1.33) and perfect thirds (5/4 or 1.25) and not seeing them for more time than I’d care to divulge. It was the process of tweaking and playing that brought me to the point of departure. After that, coming up with pitches to tune my MC banks of sign waves was nothing more than an mc.*~ object that let me set the base pitch of my oscillators and I was off to the races.

From error to epiphany

This tutorial has its beginning in a patching error. It happened while I was working on this patcher used in the early part of the previous tutorial. Here’s the original patcher with my original error intact:

At some point, I went back to working on the patch, opened it, and clicked on the startwindow message box to turn my audio on. Rather than the chordal stack I expected, my patch emitted something between a pop and a click. I realized my error right away – I’d forgotten to set my patch up so that the root note frequency number box contained a multiplier value for the ratio values. But where was the pop/click thing coming from? When I typed a value of 100. into the number box, everything was fine. But I did notice that when I clicked and scrolled the number box for a value in the single digit range, I heard a pattern of clicks spaced across the found field.

...and that’s when the light went on. I remembered an interesting talk I’d attended at an Ableton Loop event with my pal and colleague Tom Hall, where the presenter discussed the notion that two oscillators tuned to a consonant interval (say 440 and 660, which is a perfect fifth) and then lowered into the subaudible range will result in polyrhythms — in this case, a pattern of three against two, since the frequency ratio of the two pitches remains at 3/2.

Thanks to my error, I was looking at a nifty little MC-based polyrhythm generator (And here’s the interesting thing: I noticed the clicks because I’d saved my patch with the sawtooth waveforms selected. Had I saved with sine waves selected, I’d never have heard the clicks and made the connection).

Converting my original error-based patch was simplicity itself, since I’ve used the patching necessary to convert phasor~ output to bang messages for a very long time. I lopped off the top of the patch since I didn’t need any of the waveform selection logic for my generator.

I substituted an mc.phasor~ object downstream of the root note frequency multiplier and added a few scope~ objects to view the waveforms and a trio of MSP objects: change~, ==~ 1., and edge~ (to generate the bang message).

The result was an interesting and wildly variable rhythm generator that it made up for the embarrassment at my original programming infelicity. As the Oblique Strategies say,

Honor thy error as a hidden intention.

The harmonic divergence

Once I had that, the next step was to do what I suppose a lot of MC users do: since N versions of something is great, a lot more of N ought to be a lot greater, right? I’ll spare you the next hour or so, and move on to my personal answer: It might be better to look at different ways to spread my subaudio values out rather than creating a patch that channeled the ghost of a stage full of Buddy Rich clones working their kits.

So it was back to using Max’s in-app search to take a look at what else I had at my disposal in the MC theme park. And sure enough, there it was — a completely different way to specify outputs in MC, based on the Harmonic Overtone and Undertone series!

Sweeeeeeet. Once again, time to figure out how these two messages work by creating a patch to test them out. It didn't take long to patch up a bit of MC that would generate harmonics and subharmonics and let me swap between them. And — of course — I kept that magic trio of objects to translate clicks to bang messages. Here's the results: the harmonics_explorer.maxpat patch:

The results of this reminded me of a very old Steve Reich piece — which, to my knowledge — is the only one that used electronics. It was originally created as part of the Bell Laboratories partnership with artists and composers. The phase box divided a single frequency and then assigned it to notes.

It’s what the patch harmonics_player.maxpat patch does, in fact.

From resets to restless surfing

The final minor epiphany here came from doing something I do all too often: spending time listening to the output of the systems I’ve set up. Yeah, I know — I should just record everything, put out my piece/mix of the week, and move on if fame and fortune is what I’ve got in mind.

Instead, I tend to sit with what I’m making - listening for patterns, watching the UI fold, spindle, and mutate, and waiting for what comes to mind. Quite a lot of the time, one emerges from that practice having sat and listened and looked and that’s it. But sometimes, something clicks….

As with my looking at the numbers from a spread message in the very first record of my MC journey, the source was unlikely: I was looking at a set of subharmonics (I’d typed 4 and 6 into the number boxes and examined the spread of the numbers and the behavior of the mc.phasor~ objects’ separate outputs) when an image of a long-ago tutorial I’d written about using Jitter matrices to visualize a data surface composed of two 2D functions laid out at right angles to one another to form a periodic surface. I was interested in generating control output based on sending a vector across the surface of the data surface (and wrapping that output at the “edges” of the surface.

As I watched the longest phasor outputs from the lowest numbers from the subharmonics, it suddenly occurred to me that there was a connection between the rate at which I traversed the surface and something like the “angle” of traversal in the data surface I'd created in that original tutorial:

• If both increments were the same (i.e. if both phasor~ rates for the two functions were the same) then I was traversing data surface at a 45 degree angle... the same rate of increase for both the X and Y coordinates.

• If I modified the rate at which the master phasor~ that drove the X and Y functions individually, I'd be doing the equivalent of traversing the data surface at a different angle defined by the difference in whatever adjustments I'd made to the X and Y rates (using a rate operator, of course): a lower rate for the X function would mean that I traversed the equivalent of my data surface at an angle that was less than 45 degrees, and a lower rate for the Y function would traverse the surface at an angle of greater than 45 degrees.

• Further, I realized that I could think of the starting phase of the X or Y function as moving the starting point of the traversal along the X or Y edge of the surface.

• And the data itself? It was just a matter of taking the separate X and Y values at their respective traversal rates and averaging them to get the point on the data surface.

Essentially I was doing something I do with LFOs all the time; I’d just never seen it that way before. That’s what you get as a reward for staring at things and listening.

With something resembling growing surprise, I realized that I’d already done most of the heavy lifting for a patch that would let me explore this idea in the previous installment of this tutorial series. It was staring me right in the face.

Here’s the patch from the first MC journey that I started with. It was my first foray into translating my standard LFO patches into MC land:

I started work by using the LFO from that tutorial.

The insides of the MC_LFO.gendsp gen~ patcher will probably be familiar to you by now — with very few changes, its passed from the last LFO tutorial on through part 1 of the MC journey tutorial. The only variant is that we’re using MC to create 8 instances of it.

I have a lot of parameters to keep track of, but here’s where MC saves me a whole lot of time: I can use the mc.combine~ object to gang multiple parameter inputs together in a way that makes sense. I’ve got 2 sets of LFOs, each with their own inputs for waveform selection, phase offset, rate multipliers, and duty cycle. The waveform and duty cycle parameters are such that the same settings will be applied to each group of four LFOs, so I can use a pair of mc.sig~ @chans 4 objects feeding into an mc.combine~ 2 object to set them all.

While there are people who love MC for the ability to create dozens of deviated sine waves at the drop of the hat, my own experience in working with MC has been that its most powerful feature lies in the way that you can radically simplify the visual complexity of your patches.

Surfing the data (and making some noise)

Let’s put it all together.

I’ve got four pairs of LFOs whose output represents the functions mapped along the X (blue) and Y (purple) axes of my data surface. Let’s look at how I can translate all that complexity into four voices of interconnected and interrelated material.

The mc.gen~ @gen MC_LFO.gendsp @chans 8 object outputs a set of 8 LFOs from the object’s left outlet. In order to get the value of each of the four positions on the surface, I’ll need to grab those LFO outlets in a specific order - LFO 1 and 5, 2 and 6, 3 and 7 and 4 and 8.

To do this, I’ll use one of the MC objects I found while spelunking that’s built for just such a task: the mc.deinterleave object 8. Since each output is a single LFO, all I need to do to output the position on my four data surfaces is to sum and average the individual outlets in groups of 2.

The mc.deinterleave 8 object performs a similar function in letting me sum and average those same 4 pairs of 2 outputs to generate a set of spikes I can use to trigger events. (And yes, I know that those spikes represent both the X and Y edges of the data surface as a single set of trigger outputs, but I liked the variety they provided.)

All of the final note formatting happens here at the very bottom. It’s composed of a gen~ patcher than handles the note/velocity/duration parameter generation, a subpatcher that unravels all that information and formats it for output, and a nifty little scale and mode patch I borrowed from my book book Step by Step: Adventures in Sequencing with Max/MSP to organize the output a bit further:

Let’s walk through them one at a time.

LFOs and spikes to notes

When it comes to converting signal-rate input into MIDI note events, there are a squillion ways to do it, and none of them are canonical or “the best." You just start with an idea and tweak it until you’re reasonably satisfied (or satisfied enough to sit with the results and play with the parameters and explore until you get your next idea). Here’s the inside of the gen~ quantize patcher:

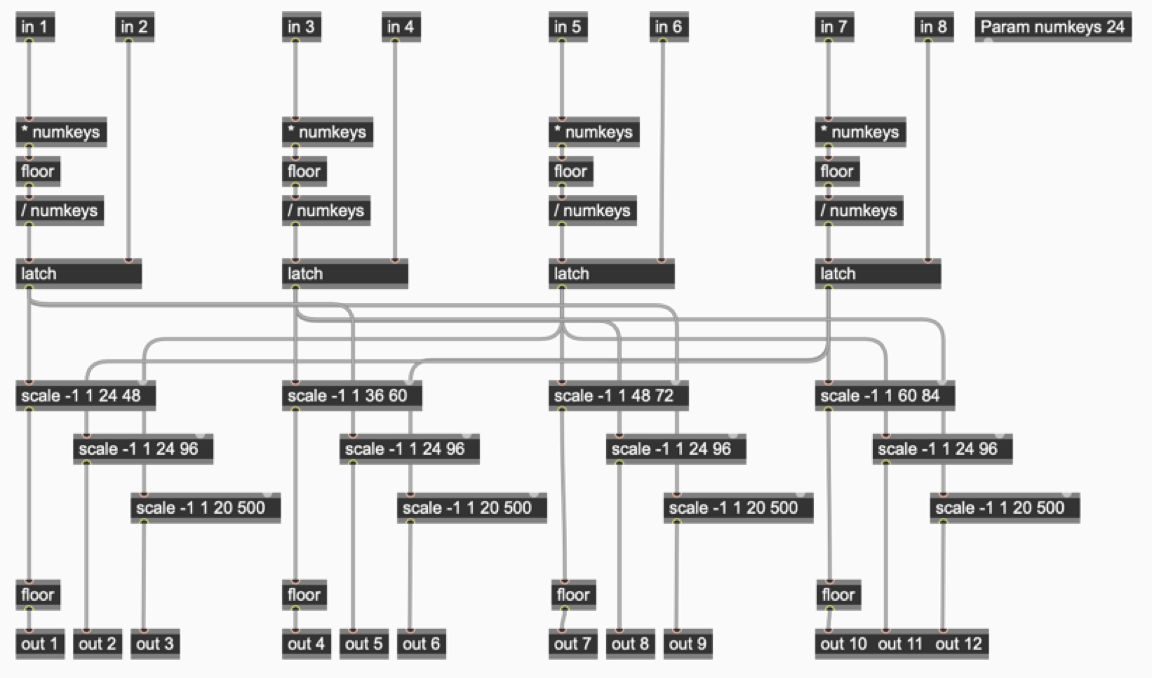
There’s nothing too fancy here, really. You’ll notice that I’m using a param object to set the range of the quantized output and then multiplying my inputs by that number, taking the non-decimal part of it (using the floor operator) and latching the result until I get a trigger input from the X or Y edges of my data surface. The latch operator outputs provide the raw materials for scale operators that give me MIDI notes, velocities, and durations. Using scaled input from different latches has the nice side effect of creating quite a bit of variety since the velocity and duration MIDI events are updated at different rates since they come from different latches, and the note is only output when the MIDI note output is sent to the makenote object (which you’ll see in the p unravel subpatcher.

Here’s what happens to all of these outputs in the p unravel subpatcher:

The subpatcher is simplicity itself: the audio-rate inputs are sampled using snapshot~. I use a Max change object to remove repeated notes. They’re finish by being formatted into four note events using makenote objects and sent on for transposition and scaling.

As I mentioned, I’ve borrowed a patch from my book Step by Step that lets you take MIDI input, increment or decrement the note numbers (which lets you start scales and modes on any starting note), choose from among a set of standard scales and modes, and specify an output key. It’s my go-to tool when I’m working in Equal Temperament. This patch is modified only in that the original in Step by Step was getting a list of note/velocity/duration info, and I’ve stripped things out to only deal with input MIDI note numbers:

Again — there’s no shame in borrowing or repurposing something you already have. It gives you more time to listen to and think about other things.

Once I got things working, it quickly became clear that some combinations worked better than others. I figured that I might benefit from creating a version of my patch intended for exploration — one that allowed me to create presets as I explored. You'll find a copy of it as LFO_datasurface_UI.maxpat.

I fired up the patch, set its output to run my Pianoteq, and settled back for some presetting time (Don't worry. I left plenty of space for you to experiment on your own).

Although I'll end this tutorial here, this is very much a work in progress — I'm thinking again about what the LFO-driven version of data surfing looks like if I fold at the X/Y boundaries instead of wrapping. But hey... I feel pretty confident about MC as a way to visually simplify my patches as I build larger structures, and the future's looking bright. Thanks for reading all this way with me. Onward!

Learn More: See all the articles in this series