Demystifying Digital Filters, Part 4

In this fourth and final installment of the Demystifying Digital Filters series, we’ll take our first steps into the implementation of IIR filter designs. While the field of recursive digital filters is enormous, understanding the basic landscape will help you to navigate and take your first steps into exploring these new territories.

This article will cover:

• Analog filter prototypes

• Methods for digitizing those prototypes

• Elementary filter sections

• Biquads and cascades

Designing IIR Filters

When we design a filter, we’re usually referring to optimizing for a set of “design” parameters such as the steepness of the transition band or the flatness of a stopband or passband. We do this by describing the filter mathematically and then solving a set of equations to get the corresponding filter coefficients.

Since analog filter design has been studied for decades, many of the most useful design equations have already been solved. These solutions are known as “filter prototypes.” Wikipedia nicely summarizes their usefulness:

The utility of a prototype filter comes from the property that all these other filters can be derived from it by applying a scaling factor to the components of the prototype. The filter design need thus only be carried out once in full, with other filters being obtained by simply applying a scaling factor.

There are a several techniques that allow us to use these prototypes in the digital domain, including:

• Impulse invariant transformation

• Bilinear transformation

• Matched Z-transform

Before we discuss these digitizing techniques though, let's look at some of the most common filter prototypes — Butterworth, Chebyshev, and elliptic.

Filter Prototypes

Keep in mind that the y-axis of these frequency response plots are in units of dB (on a logarithmic scale) so the large “bumps” are less audible than they appear. All filters represented here share the same order and cutoff value (and passband/stopband ripple allowances, as appropriate).

Butterworth Filters

The Butterworth filter is named after Stephen Butterworth, an electrical engineer who first published the design in 1930. The goal of the Butterworth filter is to achieve a maximally-flat passband — there should be no distortion or “ripples.” Out of the four prototypes here, Butterworth filters have the slowest rolloff for a given filter order.

Chebyshev Filters (Type-I and Type-II)

Chebyshev filters are named for the Chebyshev polynomials used to derive this filter design. Both Type-I and Type-II Chebyshev filters aim to minimize the error between an ideal and actual filter across the frequency response.

The rolloff of both types of filters are steeper than that of Butterworth filters — they do this by allowing ripple in the passband (for Type-I) or ripple in the stopband (for Type-II).

Type-I Chebyshev filters have slightly faster rolloffs than Type-II, but the ripple in the passband (which is likely low enough to be inaudible) may be less acceptable than ripple in the stopband.

Elliptic Filters

Elliptic filters (also known as Cauer or Zolotarev filters) have an even steeper rolloff than either of the Chebyshev filters. They achieve this by allowing ripple in both the stopband and passband. The amount of ripple in either band can be adjusted independently from the other.

Digitization Methods

Before we begin discussing digitization methods, let’s start by reminding ourselves of the distinction between analog and digital systems and signals.

In an analog signal, there is no limit to how far you can “zoom in” to find a value at any point; for any time t along the signal, there’s an exact value available. This is referred to as having a continuous-time domain.

The time domain of a digital signal, on the other hand, is discrete. This means that a finite number of samples n along the signal are defined. If you want to know the value at a point that isn’t defined, you have to use the surrounding samples and interpolate to make a reasonable guess about what that value is.

Since analog filter design equations are already available thanks to the work of electrical engineers, all we need to do is to be able to change the domain for these equations from the continuous analog representation to the discrete digital domain. If that sounds scary, just remember that you’re actually already a pro at changing domains! Any time in the course of this tutorial series that you’ve worked with a “transform” such as a Fourier transform or a Z-transform, you’ve been moving between domains. All that those transformations do is change the dependent variable of an equation by providing some kind of map between them.

For instance, you’re probably already familiar with how to transform continuous-time signals to discrete-time ones. If you have a sine wave signal f(t), in the continuous-time domain (meaning t can be any value), you would write:

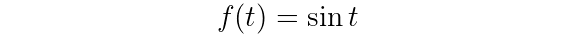
If you wanted that same signal to be transformed to the discrete-time domain (where samples are defined for integer values n), you’ll need to have some kind of relationship between t and n. The easiest way to do that is to define a constant T as the distance between samples (the sampling interval), and get the following relationship between t and n:

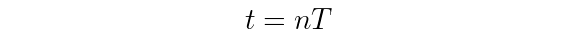
By substituting that relationship into the continuous-time signal representation, you would get back out a discrete-time representation that only depends on integer values n.

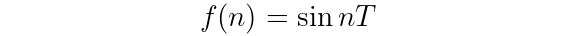
Okay, so if the relationship between continuous- and discrete-time signals is so simple, could it be just as easy to transform between continuous and discrete systems?

Here’s the bad news first: notice that when you go from analog to digital signal representations, you’re losing information. All of the data between samples in a digital signal are lost! The only way to find out the values between data points is to make some kind of educated guess as to what the value would be (using interpolation). The same goes for mapping the continuous-time equations governing analog systems to equations for digital ones. By making any kind of mapping, you will lose some fidelity with digitization.

The good news is that with digitizing analog filter prototypes, you can choose which kinds of fidelity you are willing to give up in exchange for improvements in other areas. Let’s explore the characteristics of three different transformations from the analog to the digital domain.

Impulse Invariant Transformation

The impulse invariant transformation takes a continuous-time impulse response h_c(t) from an analog filter, samples it in intervals of T, and uses that impulse h[n] as the basis for the digital filter.

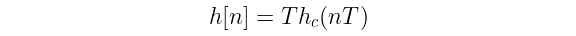
A characteristic of the impulse invariant transformation is an aliased frequency response due to the spectral folding explained by the sampling theorem.

Bilinear Transformation

The bilinear transform is mapping between the analog and digital transfer functions.

In continuous-time systems, instead of z, transfer functions use the variable s. By using the following relationship between s and z, you can take an analog transfer function (in terms of s) and digitize it.

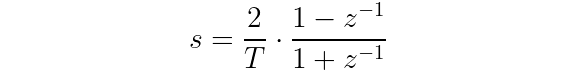
Written another way, the relationship between the analog and digital transfer functions is:

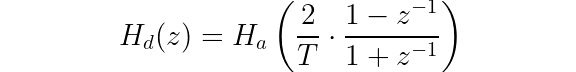
A characteristic of the bilinear transform is maintenance of stability. Since the bilinear transform maps the s-plane to the z-plane, stable poles of an analog filter will always maintain their stable position when mapped to a different domain. One downside of the bilinear transform is “frequency warping” — the frequency response of a digitized filter is slightly different from its analog counterpart.

Matched Z-transform

The matched Z-transform (also known as the root matching method) works by taking all poles and zeros s of the analog filter and mapping them to the Z-plane with the following relationship:

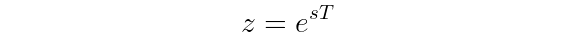
This method is simple and maintains stability of the original analog filter, but it warps both the time- and frequency-based characteristics of the digital filter result. Since that’s the case, both the impulse invariant and bilinear transforms are usually the transforms of choice for filter design.

Elementary Filter Sections

As you build higher and higher order filters, you will notice that the order of magnitude of the coefficients start to grow further apart. For example, a sixth-order filter can have some coefficients with a magnitude of 10^(-10) and others with a magnitude of 10^(-1). These differences in order of magnitude can lead to major floating point errors and numerical instability.

To minimize this kind of numerical error, higher order filters can be split up into smaller, lower order “elementary filter sections” (a term coined by your good friend Julius O. Smith III) like one-pole, one-zero, two-pole, and two-zero filters.

This “splitting” of higher order filters is possible due to two properties of transfer functions:

1. Transfer functions in series can be combined by multiplying

Imagine you are splitting up H(z) into two separate systems where the first section outputs v(n) as the input to the second section.

The transfer function of the “lumped” system is:

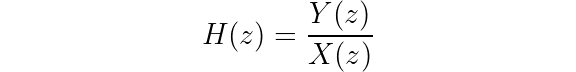
You can also separately write the transfer functions for each section in the series version.

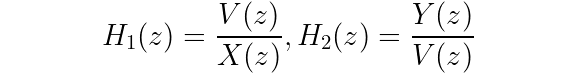
Let’s check that multiplying those transfer functions will give us the same result as the lumped system.

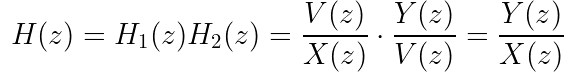
Great! This property of transfer functions is true.

2. Transfer functions in parallel can be combined by adding

How about the other case of sections in parallel?

Again, the lumped model is:

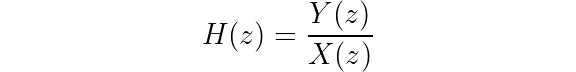
The individual sections are:

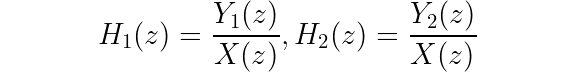
Let’s check that summing H_1 and H_2 returns the expected result.

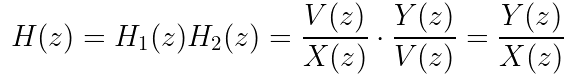
From the diagram, you can see that y_1 and y_2 sum to y, so you can now write:

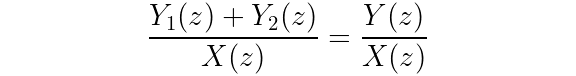
Perfect — summing sections in parallel works as expected.

To summarize, if you can turn a high order transfer function into a product of lower order transfer functions, you can take advantage of these properties and implement the higher order filter as a set of lower order filters in series. A similar idea would work for creating a sum of lower order transfer functions and implementing them as a set of parallel filters.

Biquads and Cascades — IIR in Practice

The biquadratic (“biquad”) filter is a two-pole, two-zero filter that is the workhorse building block of IIR filters. Since it is a second order filter, it provides numerical stability. Also, the digital implementation is flexible — you can easily make any of the other elementary filter sections (like a one-pole or one-zero filter) by simply using zero as a filter coefficient.

There are four different forms of the biquad filter:

• Direct form 1

• Direct form 2

• Transposed direct form 1

• Transposed direct form 2

The details of these different forms are out of the scope of this series, but it is worthwhile to know they exist since you may see different variations of the biquad out in different block diagrams. Different forms have different strengths and weaknesses, and you can learn more about them in this section of Introduction to Digital Filters with Audio Applications.

In practice, when building higher-order IIR filters, series implementations are generally preferred. This technique is known as “cascading.”

Armed with an understanding of how IIR filters are designed, you can explore the biquad~, cascade~, filterdesign, and filtergraph~ objects in Max with a better idea of what’s occurring behind the scenes. The Filter package (available from the Max Package manager) also contains a wide variety of IIR filters for both MSP and Jitter applications.

Wrapping Up

Now that you’ve made it to the end of this whirlwind tour of digital filters, you should have new insight into what a digital filter is, how one is implemented, and what design decisions can be made.

If you would like an all-in-one PDF copy of this series, check out the download below. Print it out, put it in a conspicuous place, and impress all of your friends with your new knowledge!

References

• Introduction to Digital Filters with Audio Applications and Spectral Audio Signal Processing by Julius O. Smith III

• The Scientist and Engineer's Guide to Digital Signal Processing by Steven W. Smith

• Digital Signal Processing by Alan V. Oppenheim and Ronald W. Schafer

• 2.161 Signal Processing MIT OpenCourseware

Learn More: See all the articles in this series